问题描述:
三角形的面积为S= 解:V= ![]() (S 1 +S 2 +S 3 +S 4 )r(S 1 、S 2 、S 3 、S 4 分别为四个面的面积 r为内切球半径)
(S 1 +S 2 +S 3 +S 4 )r(S 1 、S 2 、S 3 、S 4 分别为四个面的面积 r为内切球半径)
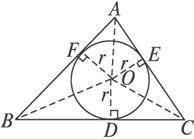
设△ABC的三边与⊙O分别切于D、E、F
则OD⊥BC OE⊥AC OF⊥AB且OD=OE=OF=r.
连结OA、OB、OC
则S △ ABC =S △ OAB +S △ OAC +S △ OBC = ![]() cr+
cr+ ![]() br+
br+ ![]() ar=
ar= ![]() (a+b+c)r.
(a+b+c)r.
类似地 三棱锥P—ABC的内切球为球O 半径为r 则球心O到各面的距离都为r
四个面的面积分别为S 1 、S 2 、S 3 、S 4
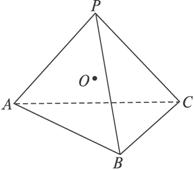
则V P—ABC =V O—ABC +V O—PBC +V O—PAC +V O—PAB
= ![]() S 1 r+
S 1 r+ ![]() S 2 r+
S 2 r+ ![]() S 3 r+
S 3 r+ ![]() S 4 r
S 4 r
= ![]() (S 1 +S 2 +S 3 +S 4 )r.
(S 1 +S 2 +S 3 +S 4 )r.

