问题描述:
P为△ABC内一点,AP,BP,CP分别交对边于D,E,F.已知AP=BP=CP=6,设PD=x,PE=y,PF=z,xy+yz+zx=28,则xyz=___.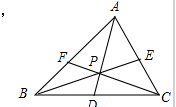
如图,作PM⊥BC,AN⊥BC,垂足分别为M,N,则S△PBCS△ABC=xx+6,S△PACS△ABC=yy+6,S△PABS△ABC=zz+6,∴xx+6+yy+6+zz+6=1∴3x+6+3y+6+3z+6=1,∴3(yz+zx+xy)+36(x+y+z)+324=xyz+6(xy+yz+zx)+36(x+y+z)+...

