问题描述:
已知矩形ABCD的长AB=4,宽AD=3,将其沿对角线BD折起,得到四面体A-BCD,如图所示,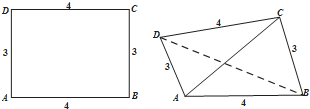
给出下列结论:
①四面体A-BCD体积的最大值为
| 72 |
| 5 |
②四面体A-BCD外接球的表面积恒为定值;
③若E、F分别为棱AC、BD的中点,则恒有EF⊥AC且EF⊥BD;
④当二面角A-BD-C为直二面角时,直线AB、CD所成角的余弦值为
| 16 |
| 25 |
⑤当二面角A-BD-C的大小为60°时,棱AC的长为
| 14 |
| 5 |
其中正确的结论的个数有( )
A. 1
B. 2
C. 3
D. 4
①四面体ABCD体积最大值为两个面互相垂直,四面体A-BCD体积的最大值为13×12×3×4×125=245,故①不正确;②三棱锥A-BCD外接球的半径为52,所以三棱锥A-BCD外接球的表面积为4π×254=25π,故②正确;③若E、F分别...

