某校数学兴趣小组为测量山高，在山脚A处测得山顶B的仰角为45°，沿着坡角为30°的山坡前进200米到达D处，在D处测得山顶B的仰角为60°，如图所示，求山的高度BC．（结果精确到1米，参考数

问题描述：

某校数学兴趣小组为测量山高，在山脚A处测得山顶B的仰角为45°，沿着坡角为30°的山坡前进200米到达D处，在D处测得山顶B的仰角为60°，如图所示，求山的高度BC．（结果精确到1米，参考数据：

2

≈1.414，

3

≈1.732）

---

最佳答案：

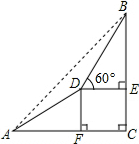
在Rt△AFD中，
∵AD=200米，∠DAF=30°，
∴DF=

1

2

AD=

1

2

×200=100（米），
AF=AD•cos30°=100

3

（米），
∵DF⊥AC，DE⊥BC，
∴四边形DFCE是矩形，
∴EC=DF=100米，
设DE=x米，则FC=x米，
在Rt△BDE中，
∵∠BDE=60°，
∴BE=tan60°•DE=

3

x（米），
∵∠BAC=45°，∠C=90°，
∴∠ABC=45°，
∴AC=BC，
∵AC=AF+FC=（100

3

+x）米，
BC=BE+EC=（

3

x+100）米，
解得：x=100，
∴BC=BE+EC=100

3

+100≈273（米），
答：山的高度BC约为273米．