如图1，为美化校园环境，某校计划在一块长为100米，宽为60米的长方形空地上修建一个长方形花圃，并将花圃四周余下的空地修建成同样宽的通道，设通道宽为a米﹒（1）用含a的式子表示花

问题描述：

如图1，为美化校园环境，某校计划在一块长为100米，宽为60米的长方形空地上修建一个长方形花圃，并将花圃四周余下的空地修建成同样宽的通道，设通道宽为a米﹒
（1）用含a的式子表示花圃的面积；
（2）如果通道所占面积是整个长方形空地面积的

1

4

，求出此时通道的宽；
（3）已知某园林公司修建通道的单价是50元/米²，修建花圃的造价y（元）与花圃的修建面积S（m²）之间的函数关系如图2所示，并且通道宽a（米）的值能使关于x的方程

1

4

x²-ax+25a-150有两个相等的实根，并要求修建的通道的宽度不少于5米且不超过12米，如果学校决定由该公司承建此项目，请求出修建的通道和花圃的造价和为多少元？

---

最佳答案：

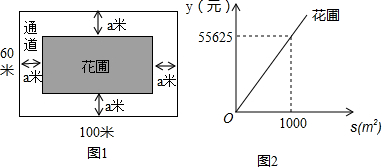
（1）由图可知，花圃的面积为（100-2a）（60-2a）=4a2-320a+6000；

（2）由已知可列式：100×60-（100-2a）（60-2a）=

1

4

×100×60，
解得：a1=5，a2=75（舍去），所以通道的宽为5米；

（3）∵方程

1

4

x2-ax+25 a-150=0有两个相等的实根，
∴△=a2-25a+150=0，解得：a1=10，a2=15，
∵5≤a≤12，
∴a=10．
设修建的花圃的造价为y元，y=55.625S；
当a=10时，S花圃=80×40=3200（m2）；y花圃=3200×55.625=178000（元），
S通道=100×60-80×40=2800（m2）；y通道=2800×50=140000（元），
造价和：178000+140000=318000（元）．