问题描述:
在平面直角坐标系x o y中已知点m n的坐标分别为负一二二一若抛物线、Y等于A X平方加x加二a不等于零与线段m n有两个不同的交点则a的取值范围
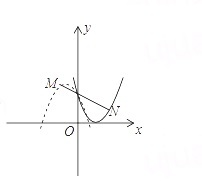
答案是,a≤-1或4分之1≤a<3分之1
解:抛物线的解析式为y=ax2-x+2.
观察图象可知当a<0时,x=-1时,y≤2时,满足条件,即a+3≤2,即as-1;当a>0时,x=2时,y≥1,且抛物线与直线MN有交点,满足条件,所以a大于等于4分之1,因为直线MN的解析式为y=-3分之1x+3分之5,
由y=-3分之1x+3分之5
y=ax的平方-x+2
消去y得到,3ax的平方-2x+1=0
因为三角形大于0,所以a<3分之1,4分之1,
所以4分之1≤a小于3分之1满足条件,
综上所述,满足条件的a的值为a≤-1或4分之1≤a<3分之1。

