问题描述:
如图
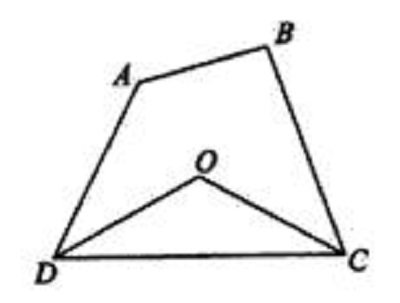
解:∵四边形的内角和为360°,
又∵∠A+∠B=222°,
∴∠ADC+∠BCD=360°-222°=138°
又∵DO、CO分别为∠ADC与∠BCD的角平分线,
∴∠ODC=1/2∠ADC,∠CCD=1/2∠BCD,
∴∠ODC+∠CCD=1/2(∠ADC+∠BCD)=1/2×138°=69°,
∴∠DOC=180°-69°=111°。
如图所示,四边形ABCD中,∠A+∠B=222°,且∠ADC\∠DCB的角平分线相交于点O,求∠COD的度数。
问题描述:
如图

解:∵四边形的内角和为360°,
又∵∠A+∠B=222°,
∴∠ADC+∠BCD=360°-222°=138°
又∵DO、CO分别为∠ADC与∠BCD的角平分线,
∴∠ODC=1/2∠ADC,∠CCD=1/2∠BCD,
∴∠ODC+∠CCD=1/2(∠ADC+∠BCD)=1/2×138°=69°,
∴∠DOC=180°-69°=111°。