问题描述:
.
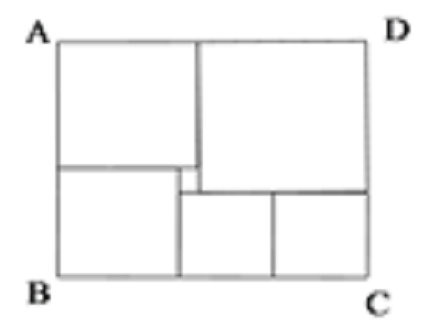
解法一:
设最大的边长为x,最小的为y,则2x-y=3x-8y=19.5
x=10.5
y=1.5
即最小边长为1.5
解法二:
设右下角的正方形的边长为x,最中间的正方形的边长为y,则有:
方程① x+3y=2x-y
方程② 3x+y=19.5
解得:x=1.5.
故最小正方形的边长为:1.5
解析:可设右下角的正方形的边长为x,最中间的正方形的边长为y,表示出其余正方形的边长,根据最大正方形边长的两种表示方法相等可得x与y的关系,再根据AD=19.5,进而得到最小正方形的边长.

