问题描述:
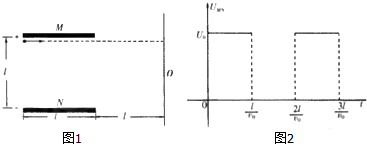
如图所示,平行金属板M,N水平放置,板右侧有一竖直荧光屏,板长,板间距及竖直屏到板右端的距离均为l,M板左下方紧贴M板有一粒子源,以初速度v0水平向右持续发射质量为m,电荷量为+q的粒子.已知板间电压UMN随时间变化的关系如图所示,其中U0=| 8mv20 |
| q |
(1)计算说明,t=0时刻射入板间的粒子打在屏上或N板上的位置;
(2)求荧光屏上发光的长度.
(1)t=0时刻射入的粒子在竖直方向做初速度为零的匀加速直线运动,
运动到下极板的时间t,l=
| 1 |
| 2 |
| qU0 |
| ml |
解得:t=
| l |
| 2v0 |
粒子在水平方向的位移:x=v0t=
| l |
| 2 |
| l |
| 2 |
(2)t=
| l |
| 2v0 |
粒子在极板间的运动时间:t1=
| l |
| v0 |
| l |
| 2v0 |
| l |
| 2v0 |
粒子离开极板时的竖直分速度:vy=at1=
| qU0 |
| ml |
粒子离开极板到打在荧光屏上的时间:t2=
| l |
| v0 |
粒子在竖直方向的偏移量:y=l+vyt2=5l,
在t=
| l |
| v0 |
离开极板后沿水平方向做匀速直线运动,粒子垂直打在荧光屏上,
这是粒子打在荧光屏的最上端位置,则荧光屏的发光长度:d=y=5l;
答:(1)t=0时刻射入板间的粒子打在N板上距N板左端
| l |
| 2 |
(2)荧光屏上发光的长度为5l.

