问题描述:
北京航天飞行控制中心对“嫦娥二号”卫星实施了降轨控制,卫星成功由轨道半径为a,周期为T1的极月圆轨道进入远月点距离为a,周期为T2的椭圆轨道,为在月球虹湾区拍摄图象做好准备,轨道如图所示.则“嫦娥二号”( )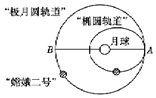
A. 在圆轨道运行周期Tl小于它在椭圆轨道运行周期T2
B. 经过圆轨道上B点时的速率大于它经过椭圆轨道上A点时的速率
C. 在圆轨道上经过A点的加速度大于在椭圆轨道上经过A点时的加速度
D. 在圆轨道上经过B点和在椭圆轨道上经过A点时的机械能相等
A、根据开普勒周期定律得:
| R3 |
| T2 |
由于圆轨道的半径大于椭圆轨道半长轴,所以在圆轨道运行周期T1大于它在椭圆轨道运行周期T2.故A错误.
B、在椭圆轨道远地点实施变轨成圆轨道是做逐渐远离圆心的运动,要实现这个运动必须万有引力小于所需向心力,所以应给“嫦娥二号”卫星加速,增加所需的向心力,所以经过圆轨道上A点时的速率大于它经过椭圆轨道上A点时的速率,而圆轨道上的各个位置速率相等,故B正确.
C、“嫦娥二号”卫星变轨前通过椭圆轨道远地点时只有万有引力来提供加速度,变轨后沿圆轨道运动也是只有万有引力来提供加速度,所以加速度相等,故C错误.
D、变轨的时候点火,发动机做功,所以“嫦娥二号”卫星点火变轨,前后的机械能不守恒,而圆轨道上的各个位置机械能相等,故D错误.
故选:B

