如图，一只总重为2000N的圆柱形油桶，底面直径为0.6m，高为0.8m，要想使油桶底部B点稍离开地面，在A点至少要施加多大的推力？

问题描述：

如图，一只总重为2000N的圆柱形油桶，底面直径为0.6m，高为0.8m，要想使油桶底部B点稍离开地面，在A点至少要施加多大的推力？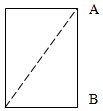

---

最佳答案：

要想使油桶底部B点稍离开地面，则应以油桶底部的左端为支点，如图：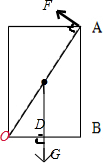

支点为点O，重力的力臂为OD=

1

2

×0.6m=0.3m，最小动力F的力臂为OA，
由勾股定理可得：OA=

(OB)2+(AB)2

=

(0.6m)2+(0.8m)2

=1m，
根据杠杆的平衡条件可得：G•OD=F•OA，
即：2000N×0.3m=F×1m，
所以F=600N．
答：最小的动力为600N．