如图所示，在绝缘水平面上的O点固定一正电荷，电荷量为Q，在离O点高度为r0的A处由静止释放一个带同种电荷、电荷量为q的液珠，液珠开始运动瞬间的加速度大小恰好为重力加速度g．已知

问题描述：

如图所示，在绝缘水平面上的O点固定一正电荷，电荷量为Q，在离O点高度为r₀的A处由静止释放一个带同种电荷、电荷量为q的液珠，液珠开始运动瞬间的加速度大小恰好为重力加速度g．已知静电力常量为k，两电荷均可看成点电荷，不计空气阻力．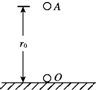

（1）求液珠开始运动瞬间所受静电力的大小和方向．
（2）求液珠运动速度最大时离O点的距离h．
（3）已知该液珠运动的最高点为B点（未标出），则当电荷量为

3q

2

的液珠仍从A 处静止释放时，问能否运动到原来的最高点B？若能，则此时经过B点的速度为多大？

---

最佳答案：

（1）液珠受到竖直向下的重力与竖直向上的库仑力作用，
由题意知，液珠的加速度大小为：a=g，
由牛顿第二定律得：F-mg=ma，
解得：F=2mg，方向：竖直向上；
（2）开始运动瞬间：F=k

qQ

r 20

=2mg，
当液珠所受合外力为零，即库仑力等于重力时，液珠的速度最大，
由平衡条件得：k

qQ

h2

=mg，
解得：h=

2

r0；
（3）能回到B点；
液珠的电荷量

3

2

q大于q，液珠受到的库仑力变大，液珠能回到B点．
液珠q从A处到B处过程中，由动能定理得：qUAB-mgr0=0-0，
电荷量为

3

2

q时，液珠从A处到B处过程中，由动能定理得：

3

2

q•UAB-mgr0=

1

2

mvB2-0，
解得：vB=

gr0

；
答：（1）液珠开始运动瞬间所受库仑力的大小为2mg，方向竖直向上；
（2）液珠运动速度最大时离O点的距离h为

2

r0；
（3）当电量为q的液此时经过B点的速度为

gr0

．