问题描述:
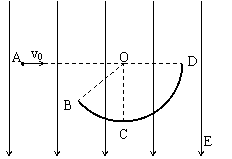
如图所示,BCD为固定在竖直平面内的半径为r=10m的圆弧形光滑绝缘轨道,O为圆心,OC竖直,OD水平,OB与OC间夹角为53°,整个空间分布着范围足够大的竖直向下的匀强电场。从A点以初速v0=9m/s沿AO方向水平抛出质量m=0.1kg的小球(小球可视为质点),小球带正电荷q=+0.01C,小球恰好从B点沿垂直于OB的方向进入圆弧轨道。不计空气阻力。求:(1)A、B间的水平距离L
(2)匀强电场的电场强度E
(3)小球过C点时对轨道的压力的大小FN
(4)小球从D点离开轨道后上升的最大高度H
(1)![]() 从A到B,vBy=v0tan53°(1分) vBy=at (1分)
从A到B,vBy=v0tan53°(1分) vBy=at (1分)
y=rcos53°(1分) ![]() y=
y=![]() at2(1分)
at2(1分)
∴t=1![]() s a=12m/s2 L=
s a=12m/s2 L=![]() v0t=9m (1分)
v0t=9m (1分)
(2)mg+qE=ma (1分) ∴E=20N/C (1分)
(3)从A到C,mar=![]() -
-![]() (1分)
(1分)
在C点,FN-ma=![]() (1分) ∴FN=4.41N (1分)
(1分) ∴FN=4.41N (1分)
(4)对全过程运用动能定理,![]()
![]() =maH (1分) ∴H=3.375m (1分)
=maH (1分) ∴H=3.375m (1分)

