如图甲所示，倾角θ=37°的粗糙斜面固定在水平面上，斜面足够长．一根轻弹簧一端固定在斜面的底端，另一端与质量m=1.0kg的小滑块（可视为质点）接触，滑块与弹簧不相连，弹簧处于压缩

问题描述：

如图甲所示，倾角θ=37°的粗糙斜面固定在水平面上，斜面足够长．一根轻弹簧一端固定在斜面的底端，另一端与质量m=1.0kg的小滑块（可视为质点）接触，滑块与弹簧不相连，弹簧处于压缩状态．当t=0时释放滑块．在0～0.24s时间内，滑块的加速度a随时间t变化的关系如图乙所示（0.24s之后的图象未画出）．已知弹簧的劲度系数k=2.0×10² N/m，当t=0.14s时，滑块的速度v₁=2.0m/s．（g取10m/s²，sin 37°=0.6，cos 37°=0.8，

5

=2.236，

6

=2.449，最大静摩擦力等于滑动摩擦力．）

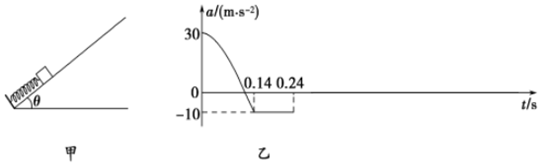
（1）斜面对滑块的摩擦力F_f
（2）t=0时弹簧的压缩量x
（3）滑块第一次离开弹簧后向上滑行的最大距离S
（4）请把0.24s后到滑块再次碰到弹簧的a-t图象在图乙中补画完整．

---

最佳答案：

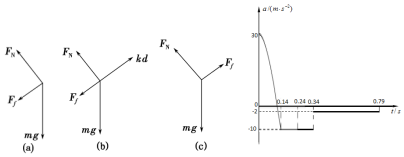（1）由图乙可知，当t1=0.14 s时，滑块与弹簧开始分离此后滑块受重力、斜面的支持力和摩擦力，如图（a）所示．
分离后，滑块开始做匀减速直线运动，在这段过程中，由图乙可知，滑块加速度的大小为：a1=10 m/s2
根据牛顿第二定律有：
mgsin θ+Ff=ma1
代入数据解得：Ff=4N
（2）由图乙可知，在出发点时滑块加速度的大小为：a=30 m/s2
此时滑块受力如图（b）所示，有：kx-mgsin θ-Ff=ma
代入数据解得：x=0.20 m
（3）设从t1=0.14 s时开始，经时间△t1滑块的速度减为零，则有：
△t1=

0-v1

-a1

=

2

10

s=0.20 s
在这段时间内滑块运动的距离为：
S=

0- v 21

2(-a1)

=

22

2×10

m=0.20 m
（4）即知t2=0.34 s时滑块速度减为零，此后滑块将反向做匀加速直线运动，受力如图c所示，根据牛顿第二定律可求得此后加速度的大小为：
a2=

mgsinθ-Ff

m

代入数据解得：a2=2.0 m/s2
设滑块沿斜面下滑回到弹簧原长处的时间为△t2
x1=

1

2

a2△t22．
解得：△t2=

5

5

s≈0.45s
所以滑块第一次离开弹簧到再次碰到弹簧的时刻为：t3=t2+△t2=0.79s
故滑块第一次离开弹簧到再次碰到弹簧的a-t图象如图所示．
答：（1）斜面对滑块的摩擦力Ff是4N．
（2）t=0时弹簧的压缩量x是0.20m．
（3）滑块第一次离开弹簧后向上滑行的最大距离S是0.20 m．
（4）如图所示．