问题描述:
如图所示,直角坐标系xOy平面竖直,y轴竖直向上,平面内有沿竖直方向的匀强电场(图中未画出),由x轴上的点A(-1,0)沿与x轴正方向成45°角以速度v=2| 2 |
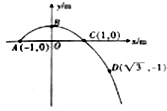
(1)B点的坐标;
(2)匀强电场的电场强度大小和方向;
(3)小球运动到D点时的速度大小和方向.
(1)由几何知识可知,小球从A点运动的B点的逆过程做类平抛运动,则有:
水平方向分速度:vAx=vAcos45°
竖直分速度:vAy=vAsin45°
水平方向做匀速运动,则有:vAxt1=xA
竖直方向做匀加速直线运动,则有:
| vAy |
| 2 |
联立解得t1=0.5s,
yB=0.5m
所以B点的坐标为(0,0.5);
(2)由类平抛运动的知识可知:
对竖直方向分析有:yB=
| 1 |
| 2 |
解得:a=4m/s2
因为加速度a=4m/s2<g,所以小球受到的电场力向上,又因为小球带负电,所以电场方向竖直向下
由牛顿第二定律可知:mg-Eq=ma
解得:E=6N/C;
(3)小球从B点到D点的运动过程做类平抛运动,由动能定理可知:
(mg-Eq)(yB+yD)=
| 1 |
| 2 |
其中vB=vAx=2m/s
解得:vD=4m/s
而vDx=vB
所以小球在D点时的速度方向与x轴正方向的夹角θ满足
cosθ=
| vDx |
| vD |
| 1 |
| 2 |
所以θ=60°.
答:(1)B点的坐标为(0,0.5);
(2)匀强电场的电场强度大小为6N/C,和方向竖直向下;
(3)小球运动到D点时的速度大小为4m/s,方向与水平方向成60°角.

