问题描述：
如图所示，在xOy平面内存在I、II、III、IV四个场区，y轴右侧存在匀强磁场I，y轴左侧与虚线MN之间存在方向相反的两个匀强电场，II区电场方向竖直向下，III区电场方向竖直向上，P点是MN与x轴的交点．有一质量为m，带电荷量+q的带电粒子由原点O，以速度v
0沿x轴正方向水平射入磁场I，已知匀强磁场I的磁感应强度垂直纸面向里，大小为2B
0，匀强电场II和匀强电场III的电场强度大小均为E=
，如图所示，IV区的磁场垂直纸面向外，大小为B
0，OP之间的距离为
，已知粒子最后能回到O点．
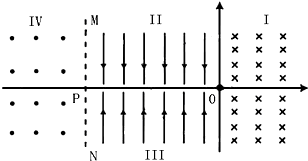
（1）带电粒子从O点飞出后，第一次回到x轴时的位置和时间；
（2）根据题给条件画出粒子运动的轨迹；
（3）带电粒子从O点飞出后到再次回到O点的时间．
最佳答案： （1）带电粒子在磁场I中运动的半径为：R1=
带电粒子在I磁场中运动了半个圆，回到y轴的坐标为：y=2R1=
带电粒子在II场区作类平抛运动，根据牛顿第二定律得带电粒子运动的加速度为：a=
=
，
竖直方向y=
at2，水平位移x=v0t，
联立得t=
，t总=
+
，第一次回到x轴的位置（-
，0）
（2）根据运动的对称性画出粒子在场区III的运动轨迹如图所示．
带电粒子在场区IV运动的半径是场区I运动半径的2倍，
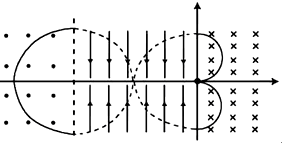
画出粒子的运动轨迹，同样根据运动的对称性画出粒子回到O点的运动轨迹如图所示．
（3）带电粒子在I磁场中运动的时间正好为1个周期，故有：t1=
带电粒子在II、III两个电场中运动的时间为：t2=4t=
带电粒子在IV场中运动的时间为半个周期为：t3=
因此带电粒子从O点飞出后到再次回到O点的时间为：t总=t1+t2+t3=
答：（1）带电粒子从O点飞出后，第一次回到x轴时的位置（-
，0），时间
+
| πm |
2qB 作业帮用户 2017-09-11  扫描下载二维码  |
