问题描述:
如图为福州一中某同学设计的一套自动传送系统,逆时针转动的传送带长L=16m,在A端有一离传送带很近的固定挡板,有一质量m=1kg的货箱与传送带间的动摩擦因数μ=0.2,自动装货系统将质量M=15kg的货物装入货箱,货物与货箱在传送带的作用下由静止从A端向B端运动,到B端时无能量损失得滑上光滑水平面并压缩轻弹簧,当弹簧被压缩至最短时自动卸货系统立即将货物卸下,然后货箱被弹回到A端,已知重力加速度g=10m/s2,则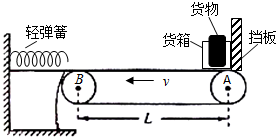
(1)若传送带转动的速度为4m/s,求货物和货箱从传送带A端运动到B端所用的时间.
(2)若为了使货箱从开始至回到A端过程中,在传送带上运动时所用时间最短,则传送带转动的速度要满足什么条件?
(3)若传送带转动的速度为5m/s,假设货箱回到A端与挡板碰撞时无能量损失,则货箱共能与挡板碰撞多少次?
(1)设货物与货箱一起向左运动的加速度为a,由牛顿第二定律可得 a=μ(m+M)gm+M经过时间t1与传送带达到相同速度 v1=at1;此过程货箱的位移 s1=12at21由以上各式解得 t1=2s,s1=4m<16m 此...

