问题描述:
如图所示为著名的“阿特伍德机”装置示意图.跨过轻质定滑轮的轻绳两端悬挂两个质量质量均为M的物块,当左侧物块附上质量为m的小物块时,该物块由静止开始加速下落,下落h后小物块撞击挡板自动脱离,系统以v匀速运动.忽略系统一切阻力,重力加速度为g,若测出v,则可完成多个力学实验.下列关于此实验的说法,正确的是( )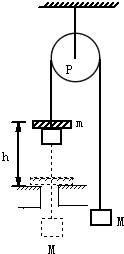
A. 系统放上小物块后,轻绳的张力增加了mg
B. 可测得当地重力加速度g=
| (2M+m)v2 |
| 2mh |
C. 要验证机械能守恒,需验证等式mgh=
| 1 |
| 2 |
D. 要探究合外力与加速度的关系,需探究mg=(M+m)
| v2 |
| 2h |
A、对系统,由牛顿第二定律得,加速度大小为:a=(M+m)g-Mg2M+m=mg2M+m.对M,由牛顿第二定律得:F-Mg=Ma,解得:F=Mg+Mmg2M+m,所以系统放上小物块后,轻绳的张力增加了Mmg2M+m,故A错误;B、对系统,由动能定理得:...

