如图所示，质量分别为m和M的两长方体物块P和Q，叠放在倾角为θ的固定斜面上．P、Q间的动摩擦因数为μ1，Q与斜面间的动摩擦因数为μ2．当它们从静止释放沿斜面滑下时，两物块始终保持相

问题描述：

如图所示，质量分别为m和M的两长方体物块P和Q，叠放在倾角为θ的固定斜面上．P、Q间的动摩擦因数为μ₁，Q与斜面间的动摩擦因数为μ₂．当它们从静止释放沿斜面滑下时，两物块始终保持相对静止，则物块P对Q的摩擦力为（　　）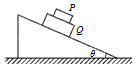

A. μ₁mgcosθ，方向平行于斜面向上

B. μ₂mgcosθ，方向平行于斜面向下

C. μ₂mgcosθ，方向平行于斜面向上

D. μ₁mgcosθ，方向平行于斜面向下

---

最佳答案：

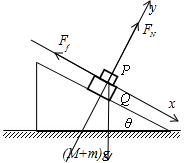对PQ整体受力分析，受到重力、支持力和滑动摩擦力，如图
根据牛顿第二定律，有：（m+M）gsinθ-μ2（m+M）gcosθ=（M+m）a
解得：a=g（sinθ-μ2cosθ）…①
再对P物体受力分析，受到重力mg、支持力和沿斜面向上的静摩擦力，根据牛顿第二定律，有
mgsinθ-Ff=ma…②
由①②解得P受到的摩擦力大小为：Ff=μ2mgcosθ，方向沿斜面向上；
根据牛顿第三定律可得物块P对Q的摩擦力为μ2mgcosθ，方向平行于斜面向下．
故ACD错误、B正确；
故选：B．