问题描述:
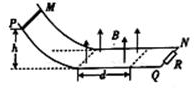
如图所示,MN和PQ是电阻不计的平行金属导轨,间距为L,导轨弯曲部分光滑,水平部分粗糙,右端接一个阻值为R的电阻.水平部分导轨左边区域有宽度为d、方向竖直向上、磁感应强度大小为B的匀强磁场.质量为m、电阻不计的金属棒从高度为h处静止释放,到达磁场右边界处恰好停止.已知金属棒与平直部分导轨间的动摩擦因数为μ,金属棒与导轨间接触良好.重力加速度为g.则金属棒穿过磁场区域的过程中( )
A. 金属棒克服安培力所做的功为mgh
B. 流过金属棒的最大电流为
C. 流过金属棒的电荷量为
D. 金属棒产生的焦耳热为mg(h-μd)
 最佳答案:
最佳答案: A、金属棒在整个运动过程中,由动能定理得:mgh-WB-μmgd=0-0,则得克服安培力做功:WB=mgh-μmgd,故A错误;
B、金属棒下滑过程中,机械能守恒,由机械能守恒定律得:mgh=
mv2,则金属棒到达水平面时的速度为:v=
金属棒到达水平面后受到向左的安培力而做减速运动,则刚进磁场时速度最大,产生的感应电动势最大,感应电流最大,最大的感应电动势为:E=BLv,最大感应电流为:I=
=
,故B正确;
C、通过定值电阻的电荷量为:q=
=
,故C错误;
D、克服安培力做功转化为焦耳热,电阻与导体棒电阻相等,通过它们的电流相等,则金属棒产生的焦耳热QR=Q=WB=mg(h-μd),故D正确.
故选:BD.


