问题描述:
如图所示,小型牵引车通过滑轮组匀速打捞起深井中的物体.在被打捞的物体没有露出水面之前,牵引车以2m/s的速度匀速行驶了10s,对绳的拉力为500N,滑轮组的机械效率为80%;当被打捞的物体完全露出水面后,滑轮组的机械效率为90%.已知物体体积为0.15m3.不计摩擦、绳重及水的阻力,不考虑物体出水后的质量变化.(取g=10N/kg)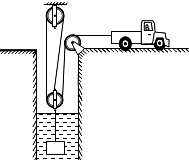
(1)被打捞的物体浸没在水中时受到的浮力是多少?
(2)物体没有露出水面之前车对绳子做了多少功?
(3)动滑轮重多少牛?
(1)被打捞的物体浸没在水中时受到的浮力:
F浮=ρ水gV排=1.0×103kg/m3×10N/kg×0.15m3=1.5×103N;
(2)物体没有露出水面之前,物体上升过程中绳的自由端移动的距离:
s=vt=2m/s×10s=20m,
车对绳子做的总功:W总=Fs=500N×20m=1×104J;
(3)由滑轮组的机械效率η=
| W有用 |
| W总 |
| W总-W额 |
| W总 |
| W额 |
| W总 |
W额=(1-η)W总=(1-80%)×1×104J=2×103J;
由图可知,动滑轮的绳子股数n=3,
则物体露出水面之前物体上升的高度:
h=
| s |
| n |
| 1 |
| 3 |
| 20 |
| 3 |
不计摩擦、绳重及水的阻力,则W额=G动h,
所以动滑轮的重力:G动=
| W额 |
| h |
| 2×103J | ||
|
答:(1)被打捞的物体浸没在水中时受到的浮力是1.5×103N;
(2)物体没有露出水面之前对绳子做了1×104J的功;
(3)动滑轮重为300N.

