问题描述:
如图所示,一水池深为h,一根长直木棍竖直地插入水底,棍露出水面部分的长度L,当太阳光与水平面夹角为60°斜射到水面时,求棍在水底的影子的长度.(已知水的折射率为n)
如图所示为光路图,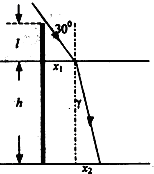
水面部分的投影长为x1=Ltan30°,
设光从空气进入水中的折射角为γ,根据折射定律得,
| sin30° |
| sinγ |
则可得cosγ=
| ||
| 2n |
| 1 | ||
|
根据几何关系可得x2=htanγ=
| h | ||
|
即棍在水底的影子长度为x=x1+x2=
| ||
| 3 |
| h | ||
|
答:棍在水底的影子的长度为
| ||
| 3 |
| h | ||
|
如图所示,一水池深为h,一根长直木棍竖直地插入水底,棍露出水面部分的长度L,当太阳光与水平面夹角为60°斜射到水面时,求棍在水底的影子的长度.(已知水的折射率为n)
问题描述:
如图所示,一水池深为h,一根长直木棍竖直地插入水底,棍露出水面部分的长度L,当太阳光与水平面夹角为60°斜射到水面时,求棍在水底的影子的长度.(已知水的折射率为n)
如图所示为光路图,
水面部分的投影长为x1=Ltan30°,
设光从空气进入水中的折射角为γ,根据折射定律得,
| sin30° |
| sinγ |
| ||
| 2n |
| 1 | ||
|
| h | ||
|
| ||
| 3 |
| h | ||
|
| ||
| 3 |
| h | ||
|