如图所示，OA为平面直角坐标系xOy第一象限内的一条射线，其将第一象限分成Ⅰ、Ⅱ两个区域，OA与x轴正方向的夹角为30°，在Ⅰ区域内存在垂直xOy平面向外的匀强磁场（未画出），磁感应强

问题描述：

如图所示，OA为平面直角坐标系xOy第一象限内的一条射线，其将第一象限分成Ⅰ、Ⅱ两个区域，OA与x轴正方向的夹角为30°，在Ⅰ区域内存在垂直xOy平面向外的匀强磁场（未画出），磁感应强度B=2×10^-5 T．在原点O处有一离子源，能沿y轴正方向射出速度大小不同的正离子，离子的比荷为

q

m

=5×10¹¹ C/kg，初速度v₀≤2×10⁶ m/s（离子的重力可忽略不计，不考虑离子间的相互作用）．

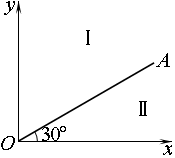
（1）求初速度v_0m=2×10⁶ m/s的离子在磁场中运动的半径r和时间t．
（2）若在（1）中的离子在磁场中运动的某时刻，在Ⅰ区域内再附加一个与原磁场同方向的匀强磁场，使离子在Ⅰ区域内做完整的圆周运动，求附加磁场的磁感应强度的最小值B₀．
（3）改变Ⅰ区域匀强磁场区域的大小，使所有从原点射出的离子经磁场偏转后均沿+x方向射出，求Ⅰ区域中匀强磁场区域的最小面积S．

---

最佳答案：

（1）离子在磁场中做圆周运动，洛伦兹力作向心力，则有Bv0mq=

mv0m2

r

，所以，r=

mv0m

Bq

=

2×106

2×10-5×5×1011

m=

1

5

m；
离子做圆周运动的周期T=

2πr

v0m

=

2πm

Bq

=

2π

2×10-5×5×1011

s=2×10-7πs；
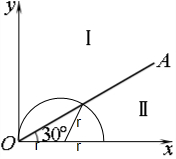
离子沿y轴正方向射入磁场，则如图所示，，粒子在磁场中转过的中心角为120°，所以，运动时间t=

1

3

T=

2

3

×10-7πs；
（2）在Ⅰ区域内再附加一个与原磁场同方向的匀强磁场，使离子在Ⅰ区域内做完整的圆周运动，粒子的运动方向不变，粒子做圆周运动的圆心在原来的半径上，则如图所示，

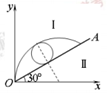
叠加磁场后磁感应强度为B，仍由洛伦兹力作向心力，所以，粒子运动的半径R=

mv0m

B′q

，则B′越小，R越大；
当半径与OA垂直时半径最大，此时，2R=r-rsin30°=

1

2

r，R=

1

4

r，B′=

mv0m

qR

=

4mv0m

qr

=4B；
所以，附加磁场的磁感应强度的最小值B0为3B=6×10-5T；
（3）所有从原点射出的离子经磁场偏转后均沿+x方向射出，所以，所有粒子转过中心角90°则射出点的纵坐标等于横坐标，则如图所示，，
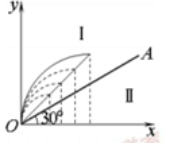
所以，Ⅰ区域中匀强磁场区域的最小面积S=

1

4

πr2-

1

2

r2=

π-2

4

r2=

π-2

4

×

1

25

m2=

π-2

100

m2．
答：（1）初速度v0m=2×106 m/s的离子在磁场中运动的半径r为

1

5

m，时间t为

2

3

×10-7πs．
（2）若在（1）中的离子在磁场中运动的某时刻，在Ⅰ区域内再附加一个与原磁场同方向的匀强磁场，使离子在Ⅰ区域内做完整的圆周运动，则附加磁场的磁感应强度的最小值B0为6×10-5T；
（3）改变Ⅰ区域匀强磁场区域的大小，�