问题描述:
在平直的公路上前后同向行驶着甲、乙两辆汽车(车长不计),甲在前,乙在后,速度大小分别为v甲、v乙,且v乙>v甲.当甲、乙两车相距L时,甲车开始以a甲的加速度大小做匀减速直线运动,为了不发生撞车事故,乙车即刻也做匀减速直线运动,则关于乙车的最小加速度的大小a乙,下列关系式可能正确的是( )A. a乙=a甲+
| (v乙-v甲)2 |
| 2L |
B. a乙=
a甲
| ||
|
C. a乙=a甲-
| (v乙-v甲)2 |
| 2L |
D. a乙=
v甲
| ||
|
若两车速度相等时,两车速度还未减为零,速度时间图线如上图所示,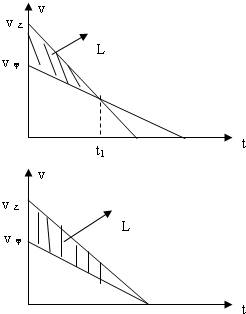
根据图线知,
| (v乙-v甲)t1 |
| 2 |
而v甲-a甲t1=v乙-a乙t1,
联立两式解得a乙≥a甲+
| (v乙-v甲)2 |
| 2L |
若乙车停止运动没有追上甲车,临界情况是静止时恰好追上甲车,速度时间图线如下图所示,
| v乙2 |
| 2a乙 |
| v甲2 |
| 2a甲 |
解得a乙≥
| a甲v乙2 |
| v甲2+2a甲L |
故选:AB.

