如图所示是倾角θ=37°的固定光滑斜面，两端有垂直于斜面的固定挡板P、Q，PQ距离L=2m，质量M=1.0kg的木块A（可看成质点）放在质量m=0.5kg的长d=0.8m的木板B上并一起停靠在挡板P处

问题描述：

如图所示是倾角θ=37°的固定光滑斜面，两端有垂直于斜面的固定挡板P、Q，PQ距离L=2m，质量M=1.0kg的木块A（可看成质点）放在质量m=0.5kg 的长d=0.8m的木板B上并一起停靠在挡板P处，A木块与斜面顶端的电动机间用平行于斜面不可伸长的轻绳相连接，现给木块A沿斜面向上的初速度，同时开动电动机保证木块A一直以初速度v₀=1.6m/s沿斜面向上做匀速直线运动，已知木块A的下表面与木板B间动摩擦因数μ₁=0.5，经过时间t，当B板右端到达Q处时刻，立刻关闭电动机，同时锁定A、B物体此时的位置．然后将A物体上下面翻转，使得A原来的上表面与木板B接触，已知翻转后的A、B接触面间的动摩擦因数变为μ₂=0.25，且连接A与电动机的绳子仍与斜面平行．现在给A向下的初速度v₁=2m/s，同时释放木板B，并开动电动机保证A木块一直以v₁沿斜面向下做匀速直线运动，直到木板B与挡板P接触时关闭电动机并锁定A、B位置．求：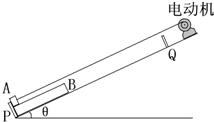

（1）B木板沿斜面向上加速运动过程的加速度大小；
（2）A、B沿斜面上升过程所经历的时间t；
（3）A、B沿斜面向下开始运动到木板B左端与P接触时，这段过程中A、B间摩擦产生的热量．

---

最佳答案：

（1）对B，由牛顿第二定律得：μ1Mgcosθ-mgsinθ=ma1，
代入数据解得：a1=2m/s2；
（2）A、B相对静止需要的时间：t1=

v0

a1

=0.8s，
A的位移：xA=v0t1=1.28m，
B的位移：xB=

v0

2

t1=0.64m，
AB的相对位移：△x=xA-xB=0.64m，
A、B匀速运动的时间：t=

L-d+△x

v0

=1.15s；
（3）B开始向下加速运动的加速度：a2=

μ2Mgcosθ+mgsinθ

m

=10m/s2，
B与A相对静止后B的加速度：a3=

mgsinθ-μ2Mgcosθ

m

=2m/s2，
A、B相对静止的时间：t2=

v1

a2

=0.2s，
A的位移：xA′=v1t2=0.4m，
B的位移：xB′=

v1

2

t2=0.2m，
相对位移：△x′=xA′-xB′=0.2m，
此时A离B右端的距离：△x′+（d-△x）=0.36m，
AB速度相等后，B以加速度a2加速运动，B到达P所用时间为t3，
则：L-d-xB=v1t3+

1

2

a2t32，
代入数据解得：t3=（

2

-1）s，
A、B相对位移：△x″=v1t3+

1

2

a2t32-v1t3=0.17m，
即：B与P接触时，A没有从B上滑离，
产生的热量：Q=μ2Mgcosθ（△x′+△x″）=0.74J；
答：（1）B木板沿斜面向上加速运动过程的加速度大小为2m/s2；
（2）A、B沿斜面上升过程所经历的时间t为1.15s；
（3）A、B沿斜面向下开始运动到木板B左端与P接触时，这段过程中A、B间摩擦产生的热量为0.74J．