问题描述:
一质量为m、两端有挡板的小车静止在光滑水平面上,两挡板间距离为1.1m,在小车正中放一质量为m、长度为0.1m的物块,物块与小车间动摩擦因数μ=0.15.如图示,现给物块一个水平向右的瞬时冲量,使物块获得v0=6m/s的水平初速度.物块与挡板碰撞时间极短且无能量损失.求: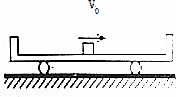
(1)小车获得的最终速度;
(2)物块相对小车滑行的路程;
(3)物块与两挡板最多碰撞了多少次;
(4)物块最终停在小车上的位置.
(1)当物块相对小车静止时,它们以共同的速度v做匀速直线运动,物块和小车相互作用过程中,系统动量守恒,
以v0的方向为正方向,根据动量守恒定律得:
mv0=(m+m)v
解得:v=3m/s
(2)对物块运动的全过程,根据动能定理得:
| 1 |
| 2 |
| 1 |
| 2 |
解得:s=6m
(3)物块第一次与小车相撞时,相对于小车运动的路程为l=
| 1.1-0.1 |
| 2 |
则相撞的次数n=
| s-0.5 |
| l-d |
| 6-0.5 |
| 1.1-0.1 |
所以物块与两挡板最多碰撞了6次
(4)根据第三问可知,相撞6次后,物块又相对小车运动了0.5m,所以小车最终还停在小车正中处.
答:(1)小车获得的最终速度为3m/s;
(2)物块相对小车滑行的路程为6m;
(3)物块与两挡板最多碰撞了6次;
(4)物块最终停在小车上的正中处.

