问题描述:
如图所示,在边长为a的正方形ABCD的对角线AC左右两侧,分别存在垂直纸面向内磁感应强度为B的匀强磁场和水平向左电场强度大小为E的匀强电场,AD、CD是两块固定荧光屏(能吸收打到屏上的粒子).现有一群质量为m、电量为q的带正电粒子,从A点沿AB方向以不同速率连续不断地射入匀强磁场中,带电粒子速率范围为| aqB |
| 12m |
| aqB |
| m |
| aqB2 |
| 12m |
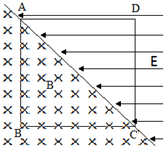
(1)带电粒子从A点射入到第一次进入电场的时间;
(2)恰能打到荧光屏C D上的带电粒子的入射速度;
(3)CD荧光屏上形成亮线的长度;
(4)AD荧光屏上形成亮线的长度.
(1)粒子在磁场中做匀速圆周运动的周期:T=
| 2πm |
| qB |
粒子进入电场时在磁场中转过的圆心角:θ=90°,
粒子从A点射入到第一次进入电场中需要的时间:t=
| θ |
| 360° |
| πm |
| 2qB |
(2)带电粒子射入匀强磁场中在洛仑兹力作用下做匀速园周运动,
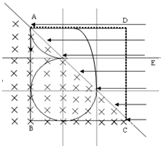
经四分之一周到达对角线沿水平向右的方向进入匀强电场,
在电场力的作用下做匀减速直线运动,
设带电粒子到达CD的速度恰好为零时对应的入射速度为V,
在磁场中的运动半径为r,由牛顿第二定律得:qvB=m
| v2 |
| r |
粒子在电场中做匀减速直线运动,由动能定理得:-qE(a-r)=0-
| 1 |
| 2 |
解得:r=
| 1 |
| 3 |
| qaB |
| 3m |
(3)由(2)可知,速度:v>
| qaB |
| 3m |
其中入射速度v=
| qaB |
| m |
| mv |
| qB |
故荧光屏CD上亮线的长度为:l1=
| 2 |
| 3 |
(4)由(2)可知,速度:v<
| qaB |
| 3m |
粒子原速返回后又在磁场中转了
| 3 |
| 4 |
在电场中类平抛运动.荧光屏AD上亮线长度为:l2=
| 2 |
| 3 |
| 1 |
| 6 |
| 1 |
| 2 |
答:(1)带电粒子从A点射入到第一次进入电场的时间为
| πm |
| 2qB |
(2)恰能打到荧光屏CD上的带电粒子的入射速度为
| qaB |
| 3m |
(3)CD荧光屏上形成亮线的长度为
| 2 |
| 3 |
(4)AD荧光屏上形成亮线的长度为
| 1 |
| 2 |

