问题描述：
某装置如图所示，两根长度均为l的轻杆OA、OB与小球以及一小滑块通过铰链连接，杆OA的A端与固定在竖直光滑杆上的铰链相连．原长也为l的轻质弹簧一端固定在A点，另一端连接小滑块，弹簧与小滑块都套在该杆上，装置静止时，弹簧长为1.6l，重力加速度为g，以下说法正确的是（ ）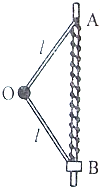
A. 轻杆OA对小球的作用力方向与竖直杆的夹角为53°
B. 轻杆OB对小滑块的作用力方向沿OB杆向下，大小为
| 5mg |
| 8 |
C. 轻杆OA与OB对小球的作用力大小之比是
| 4 |
| 3 |
D. 弹簧的劲度系数
| 5mg |
| 2l |
最佳答案： 
A、C、对球受力分析，重力，杆OA、OB对球的支持力（沿着杆的方向），
依据平行四边形定则，结合几何关系与三角知识，
则有：OA与竖直夹角为θ，
即cosθ=
| ||
| L |
解得：θ=37°，
因FA=FB，轻杆OA与OB对小球的作用力大小之比是1：1，故A错误，C错误；
B、D、对小滑块受力分析，如上图所示；
由上分析可知，FB=
| ||
| cos37° |
| 5mg |
| 8 |
依据牛顿第三定律，则轻杆OB对小滑块的作用力方向沿OB杆向下，大小为
| 5mg |
| 8 |
对于小滑块，根据平衡条件，则有：T=mg+
| 5mg |
| 8 |
| 3 |
| 2 |
再由胡克定律，则有：k=
| T |
| 1.6L-L |
| 5mg |
| 2L |
故选：BD．
