问题描述:
如图所示,质量为m1=2kg的物体甲通过三段轻绳悬挂,三段轻绳的结点为O.轻绳OA水平,OB绳与水平方向的夹角θ=30°,且通过一个光滑的轻滑轮与放置在水平面上的质量为m2=5kg的物体乙相连,物体甲、乙均处于静止状态.(g=10m/s2)求: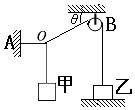
(1)轻绳OA、OB对结点O点的拉力大小;
(2)物体乙对地面的压力.
(3)滑轮轴对滑轮的弹力的大小和方向.
(1)以结点O为研究对象进行受力分析如图所示,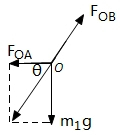
根据几何关系可得:F0A=
| m1g |
| tanθ |
| 20 | ||||
|
| 3 |
F0B=
| m1g |
| sinθ |
| 20 | ||
|
(2)对乙根据共点力的平衡条件可得:N=m2g-F0B=50N-40N=10N;
由牛顿第三定律可知:人对地面的压力N′,则N′=10 N,方向竖直向下;
(3)以滑轮轴为研究对象进行受力分析如图所示,
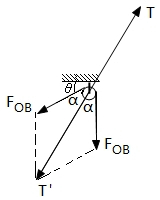
设滑轮轴对滑轮的弹力的方向与竖直方向的夹角为α,
根据几何关系可得2α=90°-30°,
解得:α=30°;
对滑轮:T=2F0B cos30°=40
| 3 |
方向与竖直方向成30°指向右上方.
答:(1)轻绳OA的拉力大小为20
| 3 |
(2)物体乙对地面的压力大小为10N,方向竖直向下;
(3)滑轮轴对滑轮的弹力的大小为40
| 3 |

