某单极发电机的简化原理如图所示．在长直线圈中垂直于线圈对称轴上固定一根半径为r的圆形金属导轨，可自由转动的金属杆CD位于线圈对称轴上，杆上固连一长为r的金属棒OA，可随杆转动

问题描述：

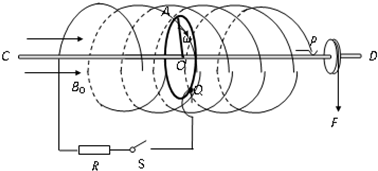
某单极发电机的简化原理如图所示．在长直线圈中垂直于线圈对称轴上固定一根半径为r的圆形金属导轨，可自由转动的金属杆CD位于线圈对称轴上，杆上固连一长为r的金属棒OA，可随杆转动，金属棒的另一端与圆形金属导轨接触良好．CD杆右侧固连一圆盘，其半径为

r

2

，并绕有细线，在恒力拉动下，圆盘和杆一起旋转．构成线圈的导线一端通过电刷P连接到杆CD上，另一端连接到圆形金属导轨Q点，回路的等效总电阻为R．线圈放置在磁感应强度为B₀的匀强磁场中，方向水平向右．（提示：当线圈中通有电流I时，电流在线圈内产生的磁感应强度大小B=aI，其中a是由线圈决定的常数）

（1）断开开关S，当金属棒转速为ω时，求金属棒OA两端电动势；
（2）闭合开关S，当金属棒以稳定转速ω₀转动时，求回路电流强度I；
（3）闭合开关S，当金属棒以稳定转速ω₀转动时，不计摩擦阻力，求作用在细线上的恒力大小F．

---

最佳答案：

（1）由法拉第电磁感应定律，则有：E=Brv=

1

2

B0ωr2
（2）线圈内总磁感应强度：B′=B0+B
而B=αI，
且I=

E

R

=B′

1

2R

ω0r2
解得：I=

B0r2ω0

2R-αr2ω0

应有：ω0<

2R

αr2

（3）金属棒稳定转动时，则有：Fv=I2R；
而v=

ω0r

2

解得：F=

2I2R

rω0

=(

B0r2ω0

2R-αr2ω0

)2•

2R

ω0

答：（1）断开开关S，当金属棒转速为ω时，金属棒OA两端电动势为

1

2

B0ωr2；
（2）闭合开关S，当金属棒以稳定转速ω0转动时，回路电流强度I为

B0r2ω0

2R-αr2ω0

；
（3）闭合开关S，当金属棒以稳定转速ω0转动时，不计摩擦阻力，作用在细线上的恒力大小F为(

B0r2ω0

2R-αr2ω0

)2•

2R

ω0

．