问题描述:
直线电机是一种利用电磁驱动原理工作的电动机械,我们可以利用以下简单的模型粗浅地理解其工作原理.如图所示,一半径为r、电阻为R的细铜环质量为m,置于水平桌面(图中未画出该桌面)的圆孔上(孔径等于环内径).另有一表面光滑的圆柱形磁棒(半径远大于绕制铜环的导线横截面的半径)竖直穿过圆孔和环,恰与孔、环不接触.磁棒产生的磁场方向沿半径方向向外,在环处的磁感应强度大小为B,磁棒下端足够长,重力加速度为g.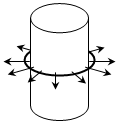
(1)若棒由静止开始竖直向上运动,其速度v与位移x的关系为v=kx(k为已知常量),当棒速度为va时环恰好对桌面压力为零,求va大小和此过程中环上产生的焦耳热Q;
(2)若棒以速度vb(vb>va)竖直向上匀速运动,环离开桌面后经时间t达到最大速度,求此时间内环上升的高度h大小;
(3)如果保持材料和半径都不变,仅将绕制铜环的铜线加粗一些,试分析说明第(2)问中铜环增加的动能如何变化.
(1)根据法拉第电磁感应定律,棒速度为va时产生的感应电动势为:E=B•2πr•va…①
感应电流为:I=
| E |
| R |
当棒速度为va时环恰好对桌面压力为零,有:BI•2πr=mg…③
①②③联立得:va=
| mgR |
| 4B2π2r2 |
速度v与位移x的关系得:va=kx…⑤
过程中环上产生的焦耳热为:Q=
| 0+mg |
| 2 |
联立④⑤⑥解得:Q=
| m2g2R |
| 8kB2π2r2 |
(2)设环的最大速度为v,则有:
E1=B•2πr•(vb-v)…⑧
产生的感应电流为:I1=
| E1 |
| R |
同理可得:
| B2(2πr)2(vb-v) |
| R |
在时间t内对环用动量定理,得:
B2(2πr)2
| ||
| R |
| . |
| △v |
h=vbt-△h…⑬
由⑧⑨⑩⑪⑫⑬联立得:
h=vbt-
(mgt+mvb-
| ||
| 4B2π2r2 |
(3)设铜的密度为ρ,电阻率为ρ电,铜线的横截面积为S,有:
m=ρ•2πr•S…⑮
R=ρ电•
| 2πr |
| S |
由⑩⑮⑯联立解得:B2(vb-v)=ρ•ρ电
所以铜环最大速度v不变,由于m增大,所以这段时间内铜环增加的动能增大.
答:(1)若棒由静止开始竖直向上运动,其速度v与位移x的关系为v=kx(k为已知常量),当棒速度为va时环恰好对桌面压力为零,va大小和此过程中环上产生的焦耳热Q为
| m2g2R |
| 8kB2π2r2 |
(2)若棒以速度vb(vb>va)竖直向上匀速运动,环离开桌面后经时间t达到最大速度,求此时间内环上升的高度h大小为vbt-
(mgt+mvb-
| ||
4B2< 作业帮用户 2017-09-20  扫描下载二维码 扫描下载二维码 |

