某同学用图（甲）所示的实验装置验证碰撞中动量守恒定律，他用两个完全相同的小钢球A、B进行实验，首先该同学使球A自斜槽某一高度由静止释放，从槽的末端水平飞出，测出球A落在水平

问题描述：

某同学用图（甲）所示的实验装置验证碰撞中动量守恒定律，他用两个完全相同的小钢球A、B进行实验，首先该同学使球A自斜槽某一高度由静止释放，从槽的末端水平飞出，测出球A落在水平地面上的点P与球飞出点在地面上竖直投影O的距离L_OP．然后该同学使球A自同一高度由静止释放，在槽的末端与静止的球B发生非对心弹性碰撞，如图（乙）．碰撞后两球向不同方向运动，测出两球落地点M、N与O点间的距离L_OM、L_ON，该同学多次重复上述实验过程，并将测量值取平均值．在忽略小球半径的情况下，对该实验的结果，分析正确的是（　　）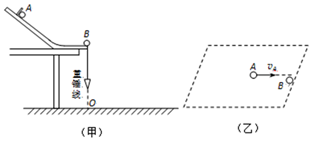

A. L_OP=L_OM+L_ON

B. L_OP²=L_OM²+L_ON²

C. OM、ON与OP间的夹角大小一定相等

D. OM与ON间夹角大小与两球碰撞的方向有关

---

最佳答案：

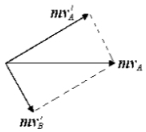设球的质量为m，碰撞前瞬间球A的速度大小为vA，碰撞后瞬间球A、B的速度大小为vA'，vB'，两球在碰撞过程中动量守恒，碰撞后两球动量的矢量与碰撞前A球动量的矢量相等，则可知，一定满足平行四边形定则，如图所示；
在弹性碰撞过程中，机械能守恒，因此有：

1

2

mvA2=

1

2

mvA'2+

1

2

mvB'2
小球做平抛运动，设时间为t，则有：
vA=

LOP

t

，v'A=

LOM

t

，vB'=

LON

t

则有：
L2OP=L2OM+L2ON
则可知，OM与ON间的夹角为90°，与碰撞方向无关，同时OM、ON与OP间的夹角大小不一定相等，故B正确，ACD错误．
故选：B．