如图所示，一个质量为m=15kg的特制柔软小猴模型，从离地面高h1=6m的树上自由下落，一辆平板车正沿着下落点正下方所在的平直路面以v0=6m/s的速度匀速前进．已知模型开始自由下落时，平板

问题描述：

如图所示，一个质量为m=15kg的特制柔软小猴模型，从离地面高h₁=6m的树上自由下落，一辆平板车正沿着下落点正下方所在的平直路面以v₀=6m/s的速度匀速前进．已知模型开始自由下落时，平板车前端恰好运动到距离下落点正下方s=3m处，该平板车总长L=7m，平板车板面离地面高h₂=1m，模型可看作质点，不计空气阻力．假定模型落到板面后不弹起，在模型落到板面的瞬间，司机刹车使平板车开始以大小为a=4m/s²的加速度做匀减速直线运动，直至停止，g取10m/s²，模型下落过程中未与平板车车头接触，模型与平板车板面间的动摩擦因数μ=0.2．求：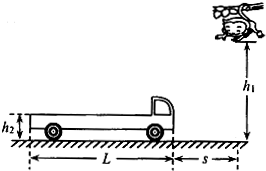

（1）模型将落在平板车上距车尾端多远处？
（2）通过计算说明，模型是否会从平板车上滑下？
（3）模型在平板车上相对滑动的过程中产生的总热量Q为多少？

---

最佳答案：

（1）设模型经时间t1下落到平板车上，由运动学公式得：h1-h2=

1

2

gt12…①
平板车在t1时间内前进的距离为x1，则：x1=v0t1…②
所以模型在车上的落点距车尾端距离：s=L+s-x1=4m…③
（2）设模型落在车上后做匀加速运动的加速度为a1，经过时间t2模型和平板车的速度相同为v，则：
平板车的速度为：v=v0-at2…④
模型的速度为：v=a1t2…⑤
对模型应用牛顿第二定律得：μmg=ma1…⑥
平板车的位移为：x2=v0t2-

1

2

at22…⑦
在这段时间内的模型的位移为：x3=

1

2

a1t22…⑧
联立③④⑤⑥⑦可得，在这段时间内模型相对车向后的位移为：
△x1=x2-x3=3m…⑨
△x1<4m…⑩
故不会滑下 
（3）速度相同后模型和平板车都减速运动直到静止，
平板车的位移为：x4=

v2

2a

…（11）
模型的位移为：x5=

v2

2a1

…（12）
模型相对车向前的位移为：△x2=x5-x4            
模型在平板上来回摩擦产生的总热量：Q=μmg（△x1+△x2）=105J…（14）
答：
（1）模型将落在平板车上距车尾端4m；
（2）通过计算说明，模型是不会从平板车上滑下；
（3）模型在平板车上相对滑动的过程中产生的总热量Q为105J．