问题描述：
如图所示，直角坐标系xOy的第一象限内有两个紧邻的半径为R的圆形区域，区域I有垂直纸面向外的匀强磁场，区域II有垂直纸面向里的匀强磁场，磁感应强度大小同为B；磁场边界上A点（A点坐标为（R，0），有一粒子源，源源不断地向磁场内发射各种方向（均平行于纸面）且速度大小相等的带正电的粒子（重力不计），粒子速度方向与X轴正方向的夹角为α，0<α<180°，已知粒子的比荷为K，速度大小为KBR，则（ ）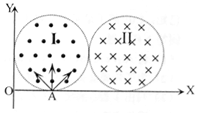
A. 全部粒子从I区域离开时的速度方向都相同
B. 全部粒子都能从II区域同一位置点飞离磁场
C. 全部粒子从A点进入磁场剑从II区域离开磁场过程中速度偏角都为180°
D. 粒子从A点进入磁场到从II区域离开磁场过程运动时间最小值为
| π |
| KB |
最佳答案： 粒子在磁场中做匀速圆周运动，洛伦兹力作向心力，则Bvq=
| mv2 |
| r |
| mv |
| Bq |
| KBR |
| BK |
| 2πr |
| v |
| 2πR |
| KBR |
| 2π |
| KB |
A、当0<α<90°时，如图所示，A点和粒子在区域Ⅰ的出射点所在的四条半径构成菱形，
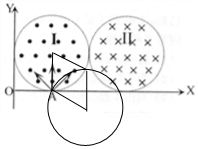，所以，粒子在区域Ⅰ转过的中心角为180°-[90°+（90°-α）]=α，所以，粒子出射速度都是水平方向；
当α=90°时，如图所示，
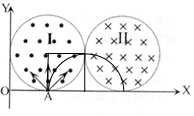，易得粒子转过中心角90°，元水平方向离开磁场区域Ⅰ；当90°<α<180°时，如图所示，A点和粒子在区域Ⅰ的出射点所在的四条半径构成菱形
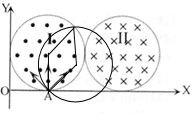，所以，粒子在区域Ⅰ转过的中心角为180°-[α-（α-90°）-（α-90°）]=α，所以，粒子出射速度都是水平方向；
综上所诉，全部粒子从I区域离开时的速度方向都是水平向右，故A正确；
BCD、当0<α<90°时，如图所示，
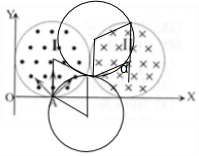，由区域Ⅰ，Ⅱ圆半径相同，粒子在两区域之间做匀速直线运动，所以，粒子进入区域Ⅱ时，径向与竖直方向的夹角为α，那么，粒子将在区域Ⅱ转过中心角180°-α，然后从区域Ⅱ边界的最高点离开磁场；当α=90°时，易得粒子将在区域Ⅱ转过中心角90°，然后从区域Ⅱ边界的最高点离开磁场；
当90°<α<180°时，如图所示，
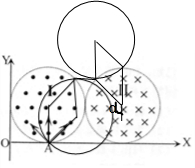，由区域Ⅰ，Ⅱ圆半径相同，粒子在两区域之间做匀速直线运动，所以，粒子进入区域Ⅱ时，径向与竖直方向的夹角为α，那么，粒子将在区域Ⅱ转过中心角180°-α，然后从区域Ⅱ边界的最高点离开磁场；所以，粒子都能从II区域最高点飞离磁场，且全部粒子从A点进入磁场剑从II区域离开磁场过程中速度偏角都为180°，故BC正确；
所以，粒子从A点进入磁场到从II区域离开磁场过程运动时间t=
| 180° |
| 360° |
| 1 |
| 2 |
| π |
| KB |
故选：ABCD．
