问题描述:
如图所示,一均匀薄板OA的长为L,质量为m,可绕O端在竖直平面内无摩擦转动,板正中间放一质量为m′的小球固定不动,一根细绳(质量不计)跨过滑轮(绳与滑轮摩擦不计),一端系于A点,另一端系在m′上,调整滑轮高度和绳子长度,使OA平衡时,板始终水平,且绳左端始终竖直,则绳子右端与水平方向成θ角.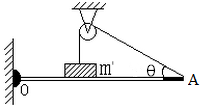
(1)画出θ=30°时绳子拉力F的力臂l,并计算力臂的大小.
(2)推导绳子拉力F与角度θ的关系式.(提示:g为定值,最后结果用题中字母表示)
(1)过支点O作拉力F作用线的垂线段,即力臂l;如图所示: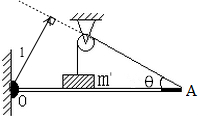
已知OA长度为L,右端细绳与水平方向成30°角,所以力臂的大小l=
| 1 |
| 2 |
(2)板正中间放一质量为m′的物体,故阻力臂L2=
| 1 |
| 2 |
以m′为研究对象,如图示,O为支点,画出各个力和力臂:
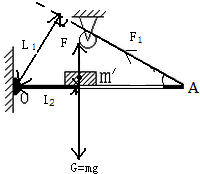
因为
| L1 |
| L |
因定滑轮不省力,故绳对物体m′的拉力大小F等于动力F1的大小,
阻力为总重力与拉力的合力,即F2=G总-F=(m+m′)g-F,
根据杠杆平衡条件F1L1=F2L2有:F×Lsinθ=[(m+m′)g-F]×
| 1 |
| 2 |
解得F=
| (m+m′)g |
| 2sinθ+1 |
答:(1)见上图;
(2)拉力F与角度θ的关系式F=
| (m+m′)g |
| 2sinθ+1 |

