问题描述：
如图所示，两平行光滑金属导轨倾斜放置且固定，两导轨间距为L，与水平面间的夹角为θ，导轨下端有垂直于轨道的挡板，上端连接一个阻值R=2r的电阻，整个装置处在磁感应强度为B、方向垂直导轨向上的匀强磁场中．两根相同的金属棒ab、cd放在导轨下端，其中棒ab靠在挡板上，棒cd在沿导轨平面向上的拉力作用下，由静止开始沿导轨向上做加速度a的匀加速运动．已知每根金属棒质量为m、电阻为r，导轨电阻不计，棒与导轨始终接触良好．求：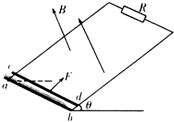
（1）经多长时间棒ab对挡板的压力变为零；
（2）棒ab对挡板压力为零时，电阻R的电功率；
（3）棒ab运动前，拉力F随时间t的变化关系．
最佳答案： （1）取ab棒为研究对象，受力分析如图所示，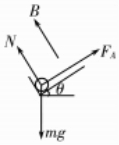
根据平衡条件可得：BIabL=mgsinθ，
设t时刻cd棒产生的电动势为E，根据法拉第电磁感应定律可得：E=BLat，
根据闭合电路的欧姆定律可得：I=
| E |
| r+R并 |
其中R并=
| 2r2 |
| 3r |
| 2r |
| 3 |
根据并联电路的特点可得：Iab=
| 2 |
| 3 |
联立解得：t=
| 5mgrsinθ |
| 2B2L2a |
（2）此时cd两端电压Ucd=E-1r，
解得：Ucd=
| mgrsinθ |
| BL |
根据电功率计算公式可得电阻R的电功率为：P=
| ||
| 2r |
联立解得：P=
| m2g2rsin2θ |
| 2B2L2 |
（3）对cd棒根据牛顿第二定律可得：F-BIL-mgsinθ=ma，
解得：F=m（gsinθ+a）+
| 3B2L2a |
| 5r |
答：（1）经
| 5mgrsinθ |
| 2B2L2a |
（2）棒ab对挡板压力为零时，电阻R的电功率为
| m2g2rsin2θ |
| 2B2L2 |
（3）棒ab运动前，拉力F随时间t的变化关系为F=m（gsinθ+a）+
| 3B2L2a |
| 5r |
