问题描述:
如图所示,水平桌面上的一柱形薄壁容器底面积为S1,内盛有密度为ρ液的某种液体后,容器及液体的总重为G1,现用一弹簧测力计悬挂一长为L、底面积为S2的柱形物体,将其缓缓进入薄壁容器的液体中(此过程中液体未溢出且柱体未浸没).图2所示为弹簧测力计示数(浸入前示数未知)随柱体底部浸入液体中深度变化的情况,请解答如下问题: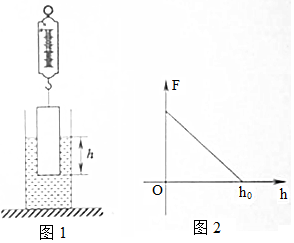
(1)写出在此过程中,柱体所受浮力F浮与其底部浸入液体深度h之间的关系式;
(2)写出此柱形物体的密度;
(3)求出在此过程中薄壁容器对水平桌面的最大压强.
(1)当柱体底部浸入液体深度为h时,柱体排开液体的体积为:V排=S2h,
由阿基米德原理可得,柱体所受的浮力:F浮=ρ液gV排=ρ液gS2h;
(2)由图2可知,柱体浸入液体的最大深度为h0,此时柱体所受浮力最大,
则最大浮力:F浮最大=ρ液gS2h0,
由图2还可知,当柱体浸入深度为h0时,拉力F=0,此时柱体处于漂浮状态,
由漂浮条件可得,柱体的重力:G物=F浮最大=ρ液gS2h0,
则柱体的质量:m物=
| G物 |
| g |
| ρ液gS2h0 |
| g |
由题可知,柱体的体积:V物=S2L,
所以,此柱形物体的密度:ρ物=
| m物 |
| V物 |
| ρ液S2h0 |
| S2L |
| ρ液h0 |
| L |
(3)此过程中液体未溢出,把容器、液体和柱体看作一个整体,整体受到向上的拉力F、向上的支持力F支和向下的总重力,由力的平衡条件可得:F+F支=G1+G物,
压力和支持力为相互作用力,其大小相等,则容器对水平桌面的压力:F压=F支=G1+G物-F,
当柱体浸入深度为h0时,拉力F=0,由上式可知,此时容器对水平桌面的压力最大,
则容器对水平桌面的最大压力为:F压最大=G1+G物=G1+ρ液gS2h0;
所以,薄壁容器对水平桌面的最大压强为:
p最大=
| F压最大 |
| S1 |
| G1+ρ液gS2h0 |
| S1 |
答:(1)此过程中,柱体所受浮力F浮与其底部浸入液体深度h之间的关系式为F浮=ρ液gS2h;
(2)此柱形物体的密度为
| ρ液h0 |
| L |
(3)在此过程中薄壁容器对水平桌面的最大压强为
| G1+ρ液gS2h0 |
| S1 |

