问题描述:
如图,A、C两点分别位于x轴和y轴上,∠OCA=30°,OA的长度为L.在△OCA区域内有垂直于xOy平面向里的匀强磁场.质量为m、电荷量为q的带正电粒子,以平行于y轴的方向从OA边射入磁场.已知粒子从某点射入时,恰好垂直于OC边射出磁场,且粒子在磁场中运动的时间为t0.不计重力.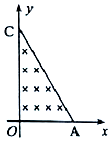
(1)求磁场的磁感应强度的大小;
(2)若粒子先后从两不同点以相同的速度射入磁场,恰好从OC边上的同一点射出磁场,求该粒子这两次在磁场中运动的时间之和;
(3)若粒子从某点射入磁场后,其运动轨迹与AC边相切,且在磁场内运动的时间为
| 4 |
| 3 |
(1)粒子在磁场中做匀速圆周运动,在时间t0内其速度方向改变了90°,故其周期
T=4t0 ①
设磁感应强度大小为B,粒子速度为v,圆周运动的半径为r.由洛伦兹力公式和牛顿定律得
qvB=m
| v2 |
| r |
匀速圆周运动的速度满足v=
| 2πr |
| T |
联立①②③式得:B=
| πm |
| 2qt0 |
(2)设粒子从OA变两个不同位置射入磁场,能从OC边上的同一点P射出磁场,粒子在磁场中运动的轨迹如图所示.
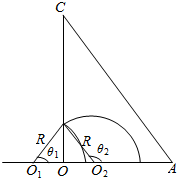
设两轨迹所对应的圆心角分别为θ1和θ2.由几何关系有
θ1=180°-θ2 ⑤
粒子两次在磁场中运动的时间分别为t1与t2,则
t1+t2=
| T |
| 2 |
(3)粒子运动轨迹如图所示,由题给条件可知,该粒子在磁场区域中的轨迹圆弧对应的圆心角为120°.
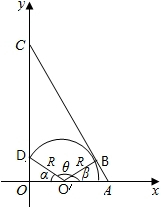
设O'为圆弧的圆心,圆弧的半径为r0,圆弧与AC相切与B点,从D点射出磁场,
由几何关系和题给条件可知,此时有
∠O O'D=∠B O'A=60° ⑦
r0cos∠OO′D+
| r0 |
| cos∠BO′A |
设粒子此次入射速度的大小为v0,
由圆周运动线速度公式,则有:v0=
4
| ||
| 13t0 |
答:(1)磁场的磁感应强度的大小为
| πm |
| 2qt0 |
(2)该粒子这两次在磁场中运动的时间之和为2t0;
(3)若粒子从某点射入磁场后,其运动轨迹与AC边相切,且在磁场内运动的时间为
| 4 |
| 3 |
4
| ||
| 13t0 |

