问题描述:
如图所示,倾角为θ=37°的固定斜面与足够长的水平面平滑对接,一劲度系数k=18N/m的轻质弹簧的上端固定于斜面顶端,另一端固连在一质量m=1kg的光滑小球A,跟A紧靠的物块B(质量也为m)与斜面间的动摩擦因数μ1=0.75,且最大静摩擦力等于滑动摩擦力,与水平面间的动摩擦因数为μ2=0.2,图中施加在B上的力F=18N,方向沿斜面向上,A和B均处于静止状态,且斜面对B恰无摩擦力,当撤除力F后,A和B一起沿斜面下滑到某处时分离,分离后A一直在斜面上运动,B继续沿斜面下滑,已知:sin37°=0.6,cos37°=0.8,重力加速度g=10m/s2,下列说法中正确的是( )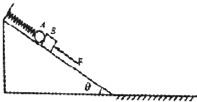
A. A和B分离后A不能回到出发点
B. A和B分离时B的速度为5m/s
C. B最终停留的位置距斜面末端1m
D. B最终停留的位置距斜面末端4m
A、A不能回到出发点,因为小球与物块一起下滑过程,物体对小球的弹力做负功而使小球和弹簧的机械能减少,故A正确.
B、未撤去力F时,对A和B整体,根据平衡条件得:
2mgsinθ+F1=F
其中弹力为:F1=kx1
解得弹簧的压缩量为:x1=
| 1 |
| 3 |
分离时,AB之间无弹力作用,但速度和加速度相等,根据牛顿第二定律,
对B:mgsinθ-f=maB
其中f=μ1mgcosθ
联立解得aB=0
对A:mgsinθ-F2=maA,
其中弹力F2=kx2
由aA=aB=0,解得分离时弹簧的伸长量为:
x2=
| 1 |
| 3 |
可见x1=x2,AB整体运动到分离弹簧的弹力做功为零,根据动能定理有:2mg•sinθ(x1+x2)-f(x1+x2)=
| 1 |
| 2 |
代入数据解得:v=2m/s.故B错误.
C、分离后由动能定理得:-μ2mgs=0-
| 1 |
| 2 |
代入数据解得s=1m,故C正确,D错误.
故选:AC.

