问题描述:
如图所示,在直角坐标系xoy的第一象限中分布着沿y轴负方向的匀强电场,在第四象限中分布着方向向里垂直纸面的匀强磁场.一个质量为m、带电+q的微粒,在A点(0,3)以初速度v0=120m/s平行x轴射入电场区域,然后从电场区域进入磁场,又从磁场进入电场,并且先后只通过x轴上的p点(6,0)和Q点(8,0)各一次.已知该微粒的比荷为| q |
| m |
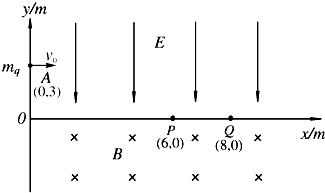
(1)微粒从A到P所经历的时间和加速度的大小;
(2)求出微粒到达P点时速度方向与x轴正方向的夹角,并画出带电微粒在电磁场中由A至Q的运动轨迹;
(3)电场强度E和磁感强度B的大小.
(1)微粒从平行x轴正方向射入电场区域,由A到P做类平抛运动,微粒在x轴上做匀速直线运动,则有 Sx=v0t
得 t=
| Sx |
| v0 |
微粒沿y轴方向做初速度为零的匀加速直线运动,有 Sy=
| 1 |
| 2 |
解得 a=2.4×103m/s2
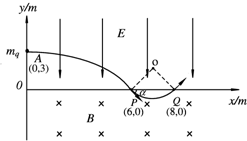
(2)微粒进入磁场时竖直方向的分速度 vy=at
由tgɑ=
| vy |
| v0 |
| at |
| v0 |
轨迹如图
(3)电场中,由牛顿第二定律得 qE=ma
解得,E=24N/C
设微粒从P点进入磁场以速度v做匀速圆周运动 v=
| 2 |
由qvB=m
| v2 |
| R |
| mv |
| qB |
由几何关系 R=
| 2 |
解得,B=
| mv |
| qR |
答:
(1)微粒从A到P所经历的时间是0.05s,加速度的大小是2.4×103m/s2;
(2)微粒到达P点时速度方向与x轴正方向的夹角是45°,画出带电微粒在电磁场中由A至Q的运动轨迹如图;
(3)电场强度E为24N/C,磁感应强度B的大小是1.2T.

