如图，场强大小为E、方向竖直向下的匀强电场中有一矩形区域abcd，水平边ab长为s，竖直边ad长为h，质量均为m、带电量分别为+q和-q的两粒子，由a、c两点先后沿ab和cd方向以速率v0进入矩形区

问题描述：

如图，场强大小为E、方向竖直向下的匀强电场中有一矩形区域abcd，水平边ab长为s，竖直边ad长为h，质量均为m、带电量分别为+q和-q的两粒子，由a、c两点先后沿ab和cd方向以速率v₀进入矩形区（两粒子不同时出现在电场中），不计重力，若两粒子轨迹恰好相切，则v₀等于（　　）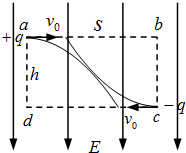

A.

s

2

2qE mh

B.

s

2

qE mh

C.

s

4

2qE mh

D.

s

4

qE mh

---

最佳答案：

由于正负粒子的质量、电荷量大小、运动初速度大小均相等，且粒子仅在电场的作用下运动，所以可知粒子做类平抛运动，且运动轨迹形状相同，根据空间的对称性可知，相切点为矩形的几何中心．
由类平抛运动的关系可得：
竖直方向：

1

2

at2=

1

2

qE

m

t2=

h

2

，
水平方向：v0t=

s

2

，
解得t=

hm qE

，
则v0=

s

2

qE hm

．
故选：B．