如图所示，等腰直角三角形abc区域中有垂直纸面向里的匀强磁场B，速度为ν0的带电粒子，从a点沿ab方向射入磁场后恰能从c点射出，现将匀强磁场B换成垂直ac边向上的匀强电场E，其它条件不

问题描述：

如图所示，等腰直角三角形abc区域中有垂直纸面向里的匀强磁场B，速度为ν₀的带电粒子，从a点沿ab方向射入磁场后恰能从c点射出，现将匀强磁场B换成垂直ac边向上的匀强电场E，其它条件不变，结果粒子仍能从c点射出，粒子的重力不计，则下列说法中正确的是（　　）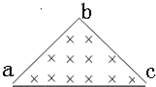

A. 粒子带正电

B.

E

B

=

2 v0

2

C. 粒子从磁场中离开时的速度方向与从电场中离开时的速度方向不同

D. 粒子从磁场中离开时的速度大小与从电场中离开时的速度大小不同

---

最佳答案：

A、B、粒子在磁场中做的是匀速圆周运动，轨迹如图所示：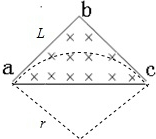

设ab=L，则轨道半径r=L
根据左手定则，粒子带负电荷；
根据牛顿第二定律，有：
qv0B=m

v 20

L

解得：
B=

mv0

qL

  ①
在电场中是类似斜抛运动，根据分运动公式，有：
y=0=v0t-

1

2

qE

m

t2（竖直分运动）
x=

2

L=v0t（水平分运动）
解得：
E=

1

2

2 mv02

qL

 ②
联立①②解得：

E

B

=

2 v0

2

；故A错误，B正确；
C、在磁场中离开C点的速度方向沿着BC方向；在电场中离开C点的速度方向也是沿着BC方向；故从磁场中离开时的速度方向与从电场中离开时的速度方向是相同的，故C错误；
D、在磁场中离开C点的速度等于初速度；在电场中，a点与C点是等势点，故离开C点的速度也等于初速度；故从磁场中离开时的速度大小与从电场中离开时的速度大小相等；故D错误；
故选：B．