问题描述:
( 20 分)薄凸透镜放在空气中时,两侧焦点与透镜中心的距离相等。如果此薄透镜两侧的介质不同,其折射率分别为 ![]() 和
和 ![]() ,则透镜两侧各有一个焦点(设为
,则透镜两侧各有一个焦点(设为 ![]() 和
和 ![]() ),但
),但 ![]() 、
、 ![]() 和透镜中心的距离不相等,其值分别为
和透镜中心的距离不相等,其值分别为 ![]() 和
和 ![]() 。现有一个薄凸透镜
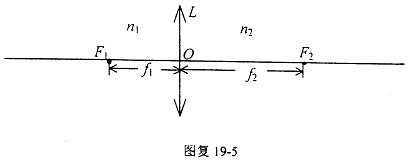
。现有一个薄凸透镜 ![]() ,已知此凸透镜对平行光束起会聚作用,在其左右两侧介质的折射率及焦点的位置如图复 19-5 所示。
,已知此凸透镜对平行光束起会聚作用,在其左右两侧介质的折射率及焦点的位置如图复 19-5 所示。
1 .试求出此时物距 ![]() ,像距
,像距 ![]() ,焦距
,焦距 ![]() 、
、 ![]() 四者之间的关系式。
四者之间的关系式。
2 .若有一傍轴光线射向透镜中心,已知它与透镜主轴的夹角为 ![]() ,则与之相应的出射线与主轴的夹角
,则与之相应的出射线与主轴的夹角 ![]() 多大?
多大?
3 . ![]() ,
, ![]() ,
, ![]() ,
, ![]() 四者之间有何关系?
四者之间有何关系?
参考解答
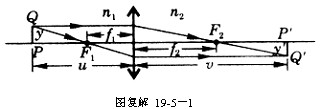
利用焦点的性质,用作图法可求得小物 ![]() 的像
的像 ![]() ,如下图所示。
,如下图所示。
(1)用 ![]() 和
和 ![]() 分别表示物和像的大小,则由图中的几何关系可得
分别表示物和像的大小,则由图中的几何关系可得
![]() (1)
(1)
![]()
简化后即得物像距公式,即 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 之间的关系式
之间的关系式
![]() (2)
(2)
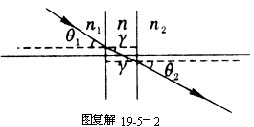
(2)薄透镜中心附近可视为筹薄平行板,入射光线经过两次折射后射出,放大后的光路如图复解19-5-2所示。图中 ![]() 为入射角,
为入射角, ![]() 为与之相应的出射角,
为与之相应的出射角, ![]() 为平行板中的光线与法线的夹角。设透镜的折射率为
为平行板中的光线与法线的夹角。设透镜的折射率为 ![]() ,则由折射定律得
,则由折射定律得
![]() (3)
(3)
对傍轴光线, ![]() 、
、 ![]() ≤1,得
≤1,得 ![]() ,
, ![]() ,因而得
,因而得
![]() (4)
(4)
(3)由物点 ![]() 射向中心
射向中心 ![]() 的入射线,经
的入射线,经 ![]() 折射后,出射线应射向
折射后,出射线应射向 ![]() ,如图复解19-5-3所示,
,如图复解19-5-3所示,
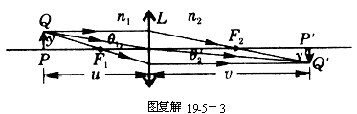
在傍轴的条件下,有
![]() (5)
(5)
二式相除并利用(4)式,得
![]() (6)
(6)
用(1)式的 ![]() 代入(6)式,得
代入(6)式,得
![]()
即 ![]() (7)
(7)
用(1)式的 ![]() 代入(6)式,得
代入(6)式,得
![]()
即 ![]() (8)
(8)
从而得 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 之间关系式
之间关系式
![]() (9)
(9)

