如图，AB是一根带铰链的轻质细杆，呈水平状态；三段轻绳的结点为B，轻绳L1与AB的夹角α=30°，其一段固定于墙壁上的C点，另一端系于B点，细绳L2的一端跨过定滑轮与原长为l0=12cm、劲度系数

问题描述：

如图，AB是一根带铰链的轻质细杆，呈水平状态；三段轻绳的结点为B，轻绳L₁与AB的夹角α=30°，其一段固定于墙壁上的C点，另一端系于B点，细绳L₂的一端跨过定滑轮与原长为l₀=12cm、劲度系数为k=400N/m的弹簧相连，弹簧另一端连接物体M，物体M静止于倾角为θ=37°，摩擦因数μ=0.5的斜面上，斜面固定于一个机械平台H上，平台的高度以及离墙竖直壁的距离均可以通过平台调节；细绳L₃下端挂有质量m_p=4kg的重物P．当调节平台，使a=β时，轻质细杆AB的上的弹力恰好为零．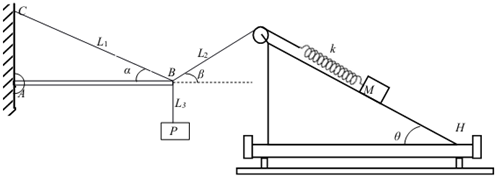

（1）求此时细绳L₂上的拉力大小以及弹簧的长度．
（2）要使物块M静止在斜面上，则物体M质量的取值范围；
（3）把物体M固定于斜面，在保证结点B的位置不变且轻质细杆AB弹力仍恰好为零的情况下，通过调节平台可使细绳L₂的拉力最小．求此时细绳L₂对结点B的拉力．

---

最佳答案：

（1）由于a=β，由受力分析可得L1和L2上的拉力大小相等，即 T1=T2，由于L1和L2的夹角为120°，则得 T1=T2=mpg=40N
弹簧的弹力 F=T2=40N
根据胡克定律：F=kx，得 x=0.1m
则弹簧的长度为 l=l0+x=0.12+0.1=0.22m=22cm
（2）当物体所受的摩擦力方向沿斜面向下且恰好达到最大静摩擦时，设此时物体的质量为m1．则有
  T2=μm1gcosθ+m1gsinθ
解得 m1=4kg
当物体所受的摩擦力方向沿斜面向上且恰好达到最大静摩擦时，设此时物体的质量为m2．则有
  T2+μm2gcosθ=m2gsinθ
解得 m2=20kg
故物体M质量的取值范围为 4kg≤M≤20kg
（3）根据三角形定则可知，当两条细绳相互垂直时，即β=60°时L2的拉力最小
最小拉力为 T2min=mPgcos30°=20

3

N
答：
（1）此时细绳L2上的拉力大小是40N，弹簧的长度是22cm．
（2）物体M质量的取值范围为 4kg≤M≤20kg．
（3）此时细绳L2对结点B的拉力是20

3

N．