问题描述:
如图所示A、B两个物体放在旋转圆台上,动摩擦因数均为μ,A的质量为3m,B的质量均为m,A离轴为R,AB间的轻绳长为R且无拉力.当圆台旋转时A、B相对圆台都没有滑动,整个过程中绳子不会断(重力加速度为g),则( )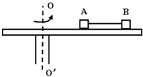
A. B物体的向心加速度最大
B. 圆台转动过程中A物体受到的静摩擦力最小
C. 只有圆台转动的角速度ω>
|
D. 为保持两物体相对圆盘静止,圆台转动的角速度不能大于
|
A、两物块A和B随着圆盘转动时,始终与圆盘保持相对静止,角速度相等,根据an=ω2r,B的转动半径大,故B的向心加速度大,故A正确;
B、当整体恰好不滑动时,两个物体的静摩擦力相等,故B错误;
C、如果没有绳子,对B物体,恰好不滑动时,有:μ(3m)g=3m
| ω | 21 |
|
同理,对物体A,恰好不滑动时,有:μmg=m
| ω | 21 |
|
故只有圆台转动的角速度ω>
|
D、对整体,恰好不滑动时,有:μ(3m+m)g=(3m)ω2(2R)+mω2R;
解得:ω=
|
为保持两物体相对圆盘静止,圆台转动的角速度不能大于
|
故选:AC

