问题描述:
打井施工时要将一质量可忽略不计的坚硬底座A送到井底,由于A与井壁间摩擦力很大,工程人员采用了如图所示的装置.图中重锤B质量为m,下端连有一劲度系数为k的轻弹簧,工程人员先将B放置在A上,观察到A不动;然后在B上再逐渐叠加压块,当压块质量达到m时,观察到A开始缓慢下沉时移去压块.将B提升至弹簧下端距井口为H0处,自由释放B,A被撞击后下沉的最大距离为h1,以后每次都从距井口H0处自由释放.已知重力加速度为g,不计空气阻力,弹簧始终在弹性限度内.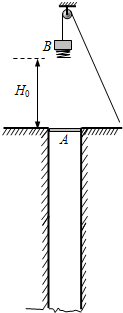
(1)求下沉时A与井壁间的摩擦力大小f和弹簧的最大形变量△L;
(2)求撞击下沉时A的加速度大小a和弹簧弹性势能Ep;
(3)若第n次撞击后,底座A恰能到达井底,求井深H.
(1)A开始缓慢下沉时,受力平衡,则有:f=2mg底座质量不计,所以合力为零,所以始终有:k△L=f解得:△L=2mgk(2)撞击后AB一起减速下沉,对B,根据牛顿第二定律得:k△L-mg=ma解得:a=g,A第一次下沉,由功能关系...

