如图所示，两条足够长的平行金属导轨倾斜放置（导轨电阻不计），倾角为30°，导轨间距为0.5m，匀强磁场垂直导轨平面向下，B=0.2T，两根材料相同的金属棒a、b与导轨构成闭合回路，a、b金

问题描述：

如图所示，两条足够长的平行金属导轨倾斜放置（导轨电阻不计），倾角为30°，导轨间距为0.5m，匀强磁场垂直导轨平面向下，B=0.2T，两根材料相同的金属棒a、b与导轨构成闭合回路，a、b金属棒的质量分别为3kg、2kg，两金属棒的电阻均为R=1Ω，刚开始两根金属棒都恰好静止，假设最大静摩擦力近似等于滑动摩擦力．现对a棒施加一平行导轨向上的恒力F=60N，经过足够长的时间后，两金属棒都达到了稳定状态．求：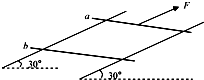

（1）金属棒与导轨间的动摩擦因数；
（2）设当a金属棒从开始受力向上运动5m时，b金属棒向上运动了2m，且此时a的速度为4m/s，b的速度为1m/s，则求此过程中回路中产生的电热及通过a金属棒的电荷量．
（3）当两金属棒都达到稳定状态时，b棒所受的安培力．

---

最佳答案：

（1）a棒恰好静止受力平衡，根据平衡条件有：
magsin300=μmagcos300
解得：μ=

3

3

；
（2）此过程对a、b棒一起根据功能关系可得：

Q=Fxa-(magsin300+μmagcos300)xa-(mbgsin300+μmbgcos300)xb

- 1 2 ma v 2a - 1 2 mb v 2b

解得；Q=85J
根据电荷量的计算公式可得：q=

.

I

•△t
根据闭合电路的欧姆定律可得：

.

I

=

. E

2R

根据法拉第电磁感应定律可得：

.

E

=

△Φ

△t

=

B•△S

△t

得q=

B•d•(xa-xb)

2R

=0.15C；
（3）两棒稳定时以相同的加速度向上匀加速直线，此时两棒有恒定的速度差．
对a棒根据牛顿第二定律可得：F-magsin300-μmagcos300-F安=ma•a，
对b棒根据牛顿第二定律可得：F安-mbgsin300-μmbgcos300=mb•a
联立解得：F安=24N．
答：（1）金属棒与导轨间的动摩擦因数为

作业帮用户 2017-09-18 扫描下载二维码