如图所示，重力不计的杠杆OAB，可绕O点在竖直平面内转动．重力为100N的物体挂在OA的中点处．已知OA=40cm，AB=30cm，OA垂直于AB，杠杆与转动轴间的摩擦忽略不计．要使杠杆平衡，且OA段

问题描述：

如图所示，重力不计的杠杆OAB，可绕O点在竖直平面内转动．重力为100N的物体挂在OA的中点处．已知OA=40cm，AB=30cm，OA垂直于AB，杠杆与转动轴间的摩擦忽略不计．要使杠杆平衡，且OA段处于水平位置，那么作用于B端的最小力的大小等于___N，并在图中画出这个最小力的示意图．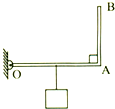

---

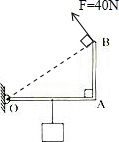最佳答案：

由题意及图示可知，当力臂为OB时，力臂最长，此时最省力
连接OB，力F垂直于OB时，力臂最大，作用力最小，如图所示；
由勾股定理可得OB=

(OA)2+(AB)2

=

(40cm)2+(30cm)2

=50cm，
由杠杆平衡条件得：G×LG=F×LF，即：G×

1

2

OA=F×OB，
F=

G× 1 2 OA

OB

=

100N× 1 2 ×40cm

50cm

=40N．
故答案为：40；见解答图．