如图所示，单匝圆形线圈与匀强磁场垂直，匀强磁场的磁感应强度为B，圆形线圈的电阻不计．导体棒a绕圆心O匀速转动，以角速度ω旋转切割磁感线，导体棒的长度为l，电阻为r．定值电阻R1

问题描述：

如图所示，单匝圆形线圈与匀强磁场垂直，匀强磁场的磁感应强度为B，圆形线圈的电阻不计．导体棒a绕圆心O匀速转动，以角速度ω旋转切割磁感线，导体棒的长度为l，电阻为r．定值电阻R₁、R₂和线圈构成闭合回路，P、Q是两个平行金属板，两极板间的距离为d，金属板的长度为L．在金属板的上边缘，有一质量为m且不计重力的带负电粒子竖直向下射入极板间，并从下边离开电场．带电粒子进入电场的位置到P板的距离为

d

3

，离开电场的位置到Q板的距离为

d

3

．

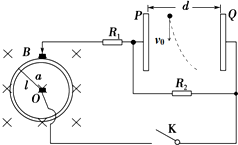
（1）导体棒a沿顺时针转动还是逆时针转动？
（2）求PQ间匀强电场的电场强度．
（3）若R₁=3r，R₂=2r，试求带电粒子的电荷量．

---

最佳答案：

（1）由题意可知，带电粒子在极板间向右偏转，粒子所受电场力向右，由于粒子带负电，极板间的场强水平向左，电路电流沿逆时针方向，由右手定则可知，导体棒a沿逆时针方向转动；
（2）导体棒a切割磁感线产生的感应电动势：ɛ=

1

2

Bl2ω，
两极板间的电压：U=IR2=

ε

R1+R2+r

R2=

Bl2ωR2

2(R1+R2+r)

，
极板间的场强为：E=

U

d

=

Bl2ωR2

2(R1+R2+r)d

；
（3）若R1=3r，R2=2r，则E=

Bl2ω

6d

，
电荷在极板间做类平抛运动，L=v0t，

1

3

d=

1

2

•

qE

m

•t2，
解得：q=

4d2m v 20

Bl2L2ω

；
答：（1）导体棒a沿逆时针转动；
（2）PQ间匀强电场的电场强度为

Bl2ωR2

2(R1+R2+r)d

；
（3）带电粒子的电荷量为

4d2m v 20

Bl2L2ω

．