如图所示，有一质量不计的轻质杠杆，左端可绕O点转动，杆上系有一悬挂重物的轻绳，重物质量为m，设轻绳可在杆上自由滑动，杆的右端用一竖直向上的动力F拉着，当物块向右匀速滑动时

问题描述：

如图所示，有一质量不计的轻质杠杆，左端可绕O点转动，杆上系有一悬挂重物的轻绳，重物质量为m，设轻绳可在杆上自由滑动，杆的右端用一竖直向上的动力F拉着，当物块向右匀速滑动时，轻质杠杆始终在水平位置保持静止．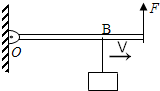

（1）在图中作出杠杆所受阻力的示意图及阻力的力臂L_阻；
（2）设悬挂重物的轻绳从杆最左端水平匀速向右滑动，试推导：说明动力F大小与滑动时间t成正比．

---

最佳答案：

（1）杠杆所受阻力为重物对杠杆的拉力，作用点在杠杆与绳的接触点上，方向竖直向下；
杠杆支点为O，过支点O做拉力的作用线的垂线段，垂线段的长即为其力臂L阻，如图所示：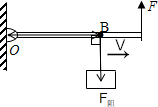

（2）设动力臂为L，根据杠杆平衡条件可得，F阻×L阻=F×L，
则F=

F阻×L阻

L

=

F阻

L

•L阻    ①
根据v=

s

t

可得，L阻=vt      ②
将②代入①可得：F=

F阻

L

•vt，
F阻=G=mg，
由上可知，

F阻

L

和v不变，动力F大小与滑动时间t成正比．
答：（1）见解答图；
（2）见解答．